وینیفرِد اِجرِتُن مِریل
24 سپتامبر 1862 – 6 سپتامبر 1951
نخستین زن آمریکایی احرازکنندهی دکترای ریاضیات
"او دری را گشود "
بر نوشتهای از عکس وینیفرِد اِجرِتُن مِریل که در دانشگاه کلُمبیا در معرض نمایش است.
سال 1886 وینیفرد اجرتن در جشن فارغالتحصیلی دانشگاه کلمبیا ایستاده بود و به تشویق رعدآسایی که او را فراگرفته بود گوش میداد. او در آن دو دقیقهی حیرتانگیز در اندیشهی چیزی بود که وی را به این لحظه رهنمون شده بود:
احراز لیسانس درجهی یک در سال 1883 از کالج وِلزلی؛ تقدیم عریضه برای حضور در دورهی دکترای ریاضی و نجوم در دانشگاه کلمبیا، که ابتدا رد شد؛ پیگیری درخواستش با هیئتامنای کلمبیا؛ ادامهی دروس عملاً بهتنهایی؛ تکمیل یک رسالهی ابتکاری دربارهی انتگرالها. و اینک اینجاست؛ نخستین بانوی آمریکایی دارای دکترای ریاضی و نخستین زن دانشآموخته از دانشگاه کلمبیا.
سفر وینیفرد اجرتن مریل سفری بود نشاندار از ذوق و پشتکار. او به نام وینیفرد اجرتن در ریپون واقع در ویسکانسین دیده به جهان گشود و پیش از شاگرداولشدنش در شانزدهسالگی با مدرک لیسانس ریاضی از کالج ولزلی، که یکی از نخستین کالجهای آمریکایی برای زنان بود، تحصیلات مقدماتی خود را نزد معلمان سرخانه گذرانده بود. او با آموزشی مختصر به بررسی مدار ستارهی دنبالهدار پُنز، که درآن زمان در رصدخانهی کالج هاروارد به بروکس موسوم بود پرداخت. وی برای ادامهی مطالعاتش خواهان تلسکوپی پرقدرت بود و برای این کار درخواست حضور در دانشگاه کلمبیا در حوزهی ریاضیات و نجوم را داد که جایی بود در سلطهی مردان.

عکسی از دانشگاه کلمبیا و رود هادسون
در نیویورک، منتشر شده در حوالی سال 1903.
کلمبیا نخستین دانشگاه آمریکا بود که به یک بانو،
وینیفرد اجرتُن، در سال 1886 دکترا تفویض نمود.
اجرتن با پسزمینهی قویای که از سالهای حضورش در وِلزلی در نجوم داشت توانست در پایاننامهی دکترایش دوام بیاورد و دوساله آن را به پایان ببرد.
او این کار را در عزلت به انجام رساند، چرا که مدیران به او اجازهی تعامل با همشاگردیهای مرد و حتی اجازهی حضور سر کلاسها را نداده بودند. وی درسگفتارها را خودش بهتنهایی میخواند. شبهای درازی را پای تلسکوپ سپری کرد و با تنهایی ساخت و عروسکهایش را همدم خویش ساخت و چون کسی به سراغش میآمد آنها را به کناری مینهاد.
جاذبهی خبری؟
هنگامی که وینیفرد در سال 1886 از کلمبیا فارغالتحصیل شد، خبرنگار نیویورک تایمز هم در آنجا حضور داشت تا از این لحظهی خطیر، و بهویژه از لباسپوشیدن او گزارش تهیه کند. براساس گزارش آنها، «لباس محجوبانهی پیادهروی به رنگ قهوهای تیره با حاشیهدوزی مخملی از همان جنس بر تن، و کلاه قهوهای حصیری با منگولهای از قیطان و پر سفید بر سر داشت.»
پایاننامهی مبتکرانهی دوبخشی او (که بخش نخست مربوط میشد به نجوم در ریاضیات) محاسبهی مدار دنبالهدار سال 1883 (دنبالهدار پُنز – بروکس) را نیز شامل میشد که برای بار دوم بود که رصد میشد. بخش دوم پایاننامه متشکل بود از ریاضیات ناب با این عنوان: "انتگرالهای چندگانه؛ (1) تعبیر هندسیشان در هندسهی دکارتی در حوزهی سهخطیها و سهوجهیها، در حوزهی مماسیها، در چهارگانیها و در هندسهی نوین؛ (2) آناکاوی ترجمان آنها در نظریهی برابریها، به کارگیری دترمینانها، ناورداییها و همورداییها در حکم ابزار تحقیق.

محوطهی رصدخانهی کالج هاروارد حدود سال 1899. مریل از تلسکوپ پرقدرتی موسوم به "انکساری بزرگ" استفاده میکرد که در سال 1847 در رصدخانه نصب شده بود. این تلسکوپ به مدت بیست سال بزرگترین تلسکوپ در ایالات متحد بود.
پایاننامهاش به واکاوی بینهایت کوچکها در سامانههای گوناگون هندسی آناکاوانه میپرداخت، از آن جمله مختصات دکارتی، مورّب، قطبی، سهخطی، سهوجهی، مماسی و چهارگانی. اجرتن کار برای یافتن بینهایت کوچکهای طول، سطح و حجم در این سامانههای گوناگون را با استفاده از رویکرد هندسی آغاز کرد. او بیان داشت که نمایش مختصات سهخطی و سهوجهی چیزی بود جدید. سپس روش تبدیلی را عرضه داشت که خلاصهی کتاب بارتولومیو پرایس در زمینهی حسابان بود و برای تبدیل انتگرالهای چندگانه از یک سامانه به دیگری به کار میرفت. بدینسان کار مبتکرانهی اِجرتُن استفاده از این شیوه بود برای تبدیل سامانهی مختصات دکارتی به مختصات سهوجهی و مماسی. اجرتن آنگاه بینهایت کوچکهای سطح و حجم را که از رویکرد هندسی همراه با شیوهی آناکاوی سامانههای گوناگون بهدستمیآمد آزمود و نشان داد که همارز هستند. افزون براین، با تبدیلات و با سامانهی چهارگانی هم کاری نو انجام شد. یکی از نتایج جدیدی که در رسالهاش بود، یافتن وابستگیهایی را شامل میشد که بین سامانههای دکارتی و مورّب و همچنین بین سامانههای مورّب و سهوجهی وجود داشت و با آنها میشد آرایههای معادلاتی مورد نیاز سامانههای دکارتی و سهوجهی را بهدست آورد.
دنبالهدار پونز – بروکس
هنگامی که ژان لویی پونز این ستارهی دنبالهدار "سحابیگون" را که در رصد 21 ژوییهی سال 1812 دنبالهی مشخصی نداشت برای نخستین بار کشف کرد، متصدی رصدخانهی مارسی در فرانسه بود. البته او تا فردای آن روز یعنی 22 ژوییه از یافتهاش گزارشی ارائه نکرد. گردش مداری این دنبالهدار 70.68 سال تخمین زده شده بود، و پس از آن در اول سپتامبر 1883 در فِلپز نیویورک بود که توسط ویلیام رابرت بروکس دیده شد. بروکس و پونز در مدت عمرشان ستارههای دنبالهدار زیادی را کشف کردند، اما پونز براساس آمار ثبتشدهی دست کم سیوهفت کشف در مدت عمرش، رکورد جهانی را شکست. دنبالهدار پونز – بروکس را در نقاطی از مدارش با چشم غیرمسلح هم میتوان دید، و به خانوادهی دنبالهدارهای هالی (Halley) وابسته است. همجواری بعدی این دنبالهدار با زمین در سال 2024 رخ خواهد داد.
پس از آنکه وینیفرد اجرتن مریل در سال 1887 با فردریک جمیز همیلتون مریل فارغالتحصیل مدرسهی معدن کلمبیا ازدواج کرد، یکی از پنج آدمی شد که در سال 1889 به تأسیس کالج بارنارد کمک کردند و این، نخستین مؤسسهی غیرمذهبی نیویورک بود که به بانوان مدرک علومانسانی میداد؛ ناگفته نماند که او خود نهایتاً مجبور شد از گروه یکپارچه مردِ آنجا استعفا دهد.
مریل در مؤسسات زیادی ریاضی تدریس کرد، و در سال 1906 مدرسهی اوکسمید را برای دختران تأسیس نمود که مدرسهای بود برای زمینهسازی راهیابیشان به کالج، و بیستودو سال برقرار ماند. مریل و شوهرش چهار فرزند داشتند. او که طرفدار دانشاندوزی زنان بود، مقالاتی نوشت و تا پیش از مرگش در سال 1951 در فِیرچایلد واقع در کانّکتیکات، سخنرانیهای وسیعی در آنباره ایراد نمود.

پرترهای از وینیفرد اجرتن مریل
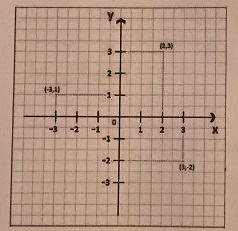
دستگاه مختصات دکارتی چیست؟
دستگاه مختصات دکارتی که در قرن هفدهم توسط رنه دکارت ابداع شد، روشی سودمند برای مکان یابی هر نقطه بین دو خط عمود برهم است. مثلاً در شکل رو به رو مختصات در ربع بالا سمت راست با 2، 3 مشخص می شود. یعنی اینکه باید دو شماره ی افقی در راستای محور X، و سه تا به بالا در راستای محور Y بروی تا مکان نقطه مشخص شود. به شکل بازی جنگ کشتی ها بدان بنگرید.
بدلیل حفظ حقوق مولف، متن کامل کتاب در این سایت ارائه نمیشود.
بخش بعدی متن را میتوانید در زنان سرکش دنیای ریاضیات - قسمت سوم مطالعه نمایید.